Définition
Un modèle hydrologique est une représentation numérique simplifiée de l’ensemble ou d’une partie des processus du cycle de l’eau (ou cycle hydrologique ; Figure 1).
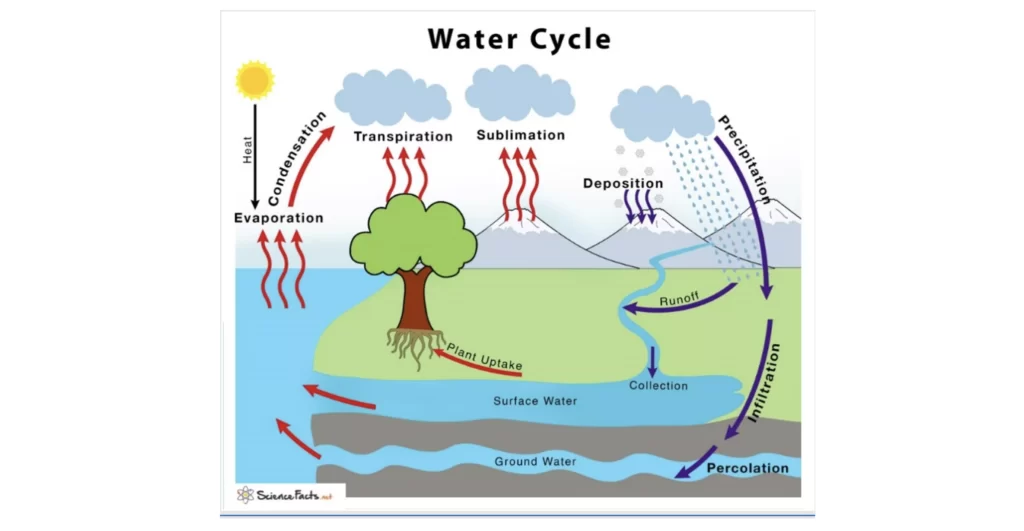
Ce cycle repose sur le bilan hydrologique, c’est à dire l’équilibre entre les entrées et les sorties en eau à l’échelle d’un bassin versant (considéré comme un système fermé). De manière générale, les entrées dans un laps de temps donné sont les précipitations qui peuvent ensuite :
- S’écouler jusqu’aux rivières, lacs et océans,
- Repartir vers l’atmosphère par évapotranspiration,
- Participer à la recharge des réserves en eau du sol, du sous-sol et des aquifères par infiltration.
L’équation générale du bilan hydrologique est la suivante :
P = Q + E + D R
avec P désignant la quantité de précipitation (liquide et solide) sur le bassin versant, Q la quantité d’eau écoulée à travers le réseau hydrographique, E la tranche d’eau retournée à l’atmosphère par évapotranspiration et DR les variations des réserves en eau du sol et du sous-sol.
Un modèle hydrologique quantifie la relation pluie-débit à l’échelle d’un bassin versant. Il permet ainsi de transformer des séries temporelles climatiques (e.g., précipitations, températures) en séries temporelles de débits ; certains modèles fournissent des informations sur d’autres processus hydrologiques (e.g., échanges nappe-rivière, écoulements souterrains, et couvert nival) ou complémentaires (e.g., qualité de l’eau).
Applications
La modélisation hydrologique a de nombreuses applications opérationnelles liées à la compréhension, la gestion et la planification de la ressource en eau. Elle permet notamment de :
- Reconstituer des séries de débits historiques,
- Modéliser des bassins versants non-jaugés,
- Analyser la réponse hydrologique d’un bassin versant, i.e., la manière dont réagit le bassin lorsqu’il est soumis à des précipitations,
- Fournir des prévisions de débits, crues et étiages,
- Evaluer l’impact des changements climatiques et environnementaux sur la ressource en eau,
- Surveiller la qualité des eaux fluviales,
- Dimensionner les infrastructures et la gestion d’ouvrages, et
- Analyser l’influence des activités humaines (e.g., construction de barrage, artificialisation des sols) sur la ressource en eau et les écosystèmes.
Chez Hydroclimat, nous utilisons la modélisation hydrologique pour fournir de la donnée eau à haute résolution spatiale. Cette donnée eau enrichie est adaptée aux études prévisionnelles et prospectives sur l’évolution de la ressource en eau et des extrêmes (crues et étiages) pour la gestion de l’eau et la planification des usages.
Tout bassin versant constitue un système hydrologique complexe de transformation des précipitations en débits par le biais de processus en interaction. Pour représenter le fonctionnement d’un bassin versant, de nombreux modèles hydrologiques ont été élaborés, fournissant chacun une représentation plus ou moins simplifiée de ce système, ayant chacun leur intérêt et leurs propres limites.
Les divers modèles hydrologiques se différencient notamment sur deux critères :
- Les options de simulations en termes de discrétisation spatiale, c’est à dire la façon de représenter le bassin versant comme une entité homogène unique (modèle global) ou en sous-unités hydrologiques (modèle semi-distribué et distribué), et
- La manière de décrire les processus hydrologiques, qui peut se faire soit par des équations empiriques, physiques, soit par une simplification plus ou moins poussée des équations physiques (approche conceptuelle).
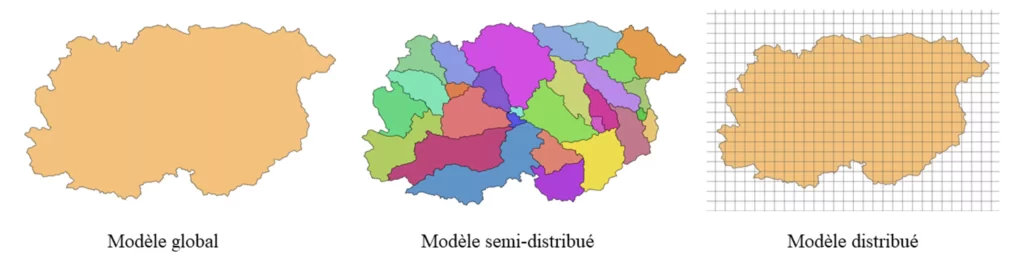
Trois types de modèles hydrologiques se différencient selon la discrétisation spatiale du bassin versant :
- Les modèles globaux : le bassin versant est décrit comme une seule entité spatiale homogène où le bilan hydrologique est moyenné à l’échelle du bassin sans tenir compte de la variabilité spatiale des processus hydrologiques et des données d’entrée.
- Les modèles semi-distribués: le bassin versant est divisé en plusieurs sous-bassins versants. Chaque sous-bassin est traité comme une unité hydrologique spatialement homogène définissant le calcul des processus hydrologiques.
- Les modèles distribués: le bassin versant est discrétisé en grille régulière ou irrégulière. Les processus hydrologiques sont calculés pour chaque cellule de la grille. Les modèles distribués sont alors plus complexes et plus exigeants en termes de données d’entrée et de temps de calcul.
Le deuxième critère de classification porte sur la représentation des processus ; trois types de modèles hydrologiques se distinguent alors :
Les modèles statistiques ou “data-driven” qui établissent un lien purement mathématique entre les variables d’entrée et de sortie du bassin versant, sans faire intervenir des données sur ses caractéristiques physiques. Ces modèles qualifiés de « boîtes noires » sont caractérisés par des paramètres et des relations statistiques avec aucune signification physique. C’est la limite essentielle de ces modèles qui conviennent peu aux études fines sur le fonctionnement ou aux études d’impact du changement climatique sur l’hydrologie d’un bassin versant. Cependant ils s’avèrent utiles pour des simulations en temps réel en raison de leur rapidité d’exécution ou pour analyser globalement le comportement d’un hydrosystème. C’est le cas par exemple des modèles stochastiques (i.e., auto-régression, régression linéaire, régression multiples), des réseaux de neurones artificiels (i.e., LSTM et GRU), du Machine Learning et autres techniques (ondelettes, théorie du chaos, etc.)
Les modèles conceptuels qui considèrent le bassin versant comme un assemblage de réservoirs interconnectés représentant plusieurs niveaux de stockage selon une dimension verticale. Ce type de modèle apparait toutefois peu réaliste : les équations décrivant l’alimentation et la vidange des réservoirs font intervenir des paramètres sans aucune signification hydrologique, qui sont souvent non corrélés aux caractéristiques du bassin versant. La valeur des paramètres est obtenue par ajustement des débits simulés aux débits mesurés. De ce fait, les modèles conceptuels fournissent des simulations de débits certes acceptables, mais ne peuvent donner des simulations correctes des autres variables hydrologiques (évapotranspiration, infiltration, recharge, etc.) qui demeurent importantes dans de nombreuses applications. Par ailleurs, ces modèles conviennent peu aux études sur l’impact des aménagements sur les hydrosystèmes et ne sont pas adaptés aux bassins versants non-jaugés. Malgré cela, ils s’avèrent être des outils efficaces pour des applications spécifiques telles que l’étude sur la ressource en eau, la prévision des crues et des étiages, à partir d’un minimum d’information et de données d’entrée sur le bassin versant étudié.
Les modèles à base physique qui viennent combler le fossé entre les modèles hydrologiques statistiques “trop descriptifs” et les modèles conceptuels à réservoirs “trop simplistes” du point de vue de l’expression des phénomènes hydrologiques. Ces modèles sont fondés sur les processus hydrologiques réels et utilisent des équations déduites des principes de base de la physique pour les représenter. Ils ont alors pour avantage d’utiliser des paramètres qui ont un sens physique, pouvant ainsi fournir une grande quantité d’informations sur les différents termes du bilan hydrologique (évapotranspiration, infiltration, recharge, etc.) du bassin versant étudié. Par leur capacité à associer des paramètres à des caractéristiques climatiques et physiques des bassins versants, les modèles physiques présentent de grands avantages dans l’interprétation et la prédiction des impacts du changement climatique sur l’hydrologie du bassin versant. Les limites majeures quant à leur application résident dans la nécessité et la qualité des nombreuses données d’entrée, à une résolution spatiale et temporelle suffisante afin d’estimer les paramètres du modèle.
Caractéristique | Type de modèle | Exemples |
|---|---|---|
Représentation du bassin versant (discrétisation) | Global | WaterGAP [1]
|
Semi-distribué | SWAT [2], VIC [3]
| |
Distribué | G2G [4], MIKE SHE [5]
| |
Description des processus hydrologiques | ||
Statistique | GR4J [6], Deep Learning-based models
| |
Conceptuel | HBV [7], TOPMODEL [8]
| |
À base physique | SWAT [2], HYPE [9]
|
Tableau 1 – Exemples de modèles hydrologiques selon les deux critères de différentiation
Le choix du type de modèle à utiliser dépend de l’objectif de l’étude ainsi que des données d’entrées disponibles. Chez Hydroclimat, nous avons fait le choix d’utiliser le modèle SWAT (Soil and Water Assessment Tool, [2]), un modèle semi-distribué à base physique qui permet de simuler la réponse hydrologique de bassins versants pouvant atteindre plusieurs milliers de km au pas de temps journalier (https://swat.tamu.edu/). Le modèle SWAT est un outil flexible et robuste, largement utilisé dans le monde entier pour évaluer, entre autres, l’évolution des ressources en eau et l’impact hydrologique de l’occupation du sol et du changement climatique.
[1] H. Müller Schmied et al., « The global water resources and use model WaterGAP v2.2d: model description and evaluation », Geosci. Model Dev., vol. 14, no 2, p. 1037‑1079, févr. 2021, doi: 10.5194/gmd-14-1037-2021.
[2] S. L. Neitsch, J. G. Arnold, J. R. Kiniry, et J. R. Williams, « Soil and Water Assessment Tool Theoretical Documentation Version 2009 », Texas Water Resources Institute, Technical Report, sept. 2011. Consulté le: 10 avril 2023. [En ligne]. Disponible sur: https://oaktrust.library.tamu.edu/handle/1969.1/128050
[3] H. Wang, Z. Wu, et C. Hu, « A Comprehensive Study of the Effect of Input Data on Hydrology and non-point Source Pollution Modeling », Water Resour. Manag., vol. 29, no 5, p. 1505‑1521, mars 2015, doi: 10.1007/s11269-014-0890-x.
[4] V. A. Bell, A. L. Kay, R. G. Jones, et R. J. Moore, « Development of a high resolution grid-based river flow model for use with regional climate model output », Hydrol. Earth Syst. Sci., vol. 11, no 1, p. 532‑549, janv. 2007, doi: 10.5194/hess-11-532-2007.
[5] M. B. Abbott, J. C. Bathurst, J. A. Cunge, P. E. O’Connell, et J. Rasmussen, « An introduction to the European Hydrological System — Systeme Hydrologique Europeen, “SHE”, 1: History and philosophy of a physically-based, distributed modelling system », J. Hydrol., vol. 87, no 1, p. 45‑59, oct. 1986, doi: 10.1016/0022-1694(86)90114-9.
[6] C. Perrin, C. Michel, et V. Andréassian, « Improvement of a parsimonious model for streamflow simulation », J. Hydrol., vol. 279, no 1, p. 275‑289, août 2003, doi: 10.1016/S0022-1694(03)00225-7.
[7] S. BERGSTROM, « The HBV Model -its structure and applications », HBV Model -Its Struct. Appl., no 4, 1992.
[8] K. J. BEVEN et M. J. KIRKBY, « A physically based, variable contributing area model of basin hydrology / Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant », Hydrol. Sci. Bull., vol. 24, no 1, p. 43‑69, mars 1979, doi: 10.1080/02626667909491834.
[9] G. Lindström, C. Pers, J. Rosberg, J. Strömqvist, et B. Arheimer, « Development and testing of the HYPE (Hydrological Predictions for the Environment) water quality model for different spatial scales », Hydrol. Res., vol. 41, no 3‑4, p. 295‑319, avr. 2010, doi: 10.2166/nh.2010.007.
Les modèles hydrologiques expriment les processus hydrologiques à l’échelle d’un bassin versant au travers d’équations qui soit sont empiriques, soit relèvent des principes de base de la physique, ou soit d’une simplification plus ou moins poussée des équations physiques. Ces équations font intervenir des paramètres qui doivent être ajustés afin de mieux représenter les particularités du bassin versant étudié. La calibration, aussi appelée calage, est le procédé par lequel ces paramètres sont ajustés de façon à ce que les résultats simulés par le modèle correspondent le mieux possible aux données observées. L’étape de calibration s’effectue sur une période historique pour laquelle des données d’observation (e.g., de débit) sont disponibles. Une période de calibration de plusieurs années est nécessaire pour caler les paramètres sur différentes saisons et pour des événements très différents.
Il existe deux types de calage :
- Le calage manuel, qui consiste à modifier manuellement et individuellement les paramètres du modèle et observer l’effet sur la simulation des débits. L’hydrologue utilise son expertise pour analyser les hydrogrammes obtenus et ajuster au mieux les paramètres du modèle afin d’aboutir à une reproduction acceptable de l’intensité et de l’occurrence des pics de débit, des volumes de crue et des débits de base.
- Le calage automatique, qui consiste à utiliser un algorithme d’optimisation pour minimiser la différence entre les valeurs simulées et celles observées. Ces optimisateurs sont basés sur des méthodes itératives et intelligentes qui modifient graduellement les paramètres du modèle et déterminent leurs valeurs optimales.
La calibration manuelle nécessite d’avoir une bonne compréhension des processus hydrologiques et de leurs interactions. Elle est cependant subjective, fastidieuse et chronophage, particulièrement lorsque le modèle comprend de nombreux paramètres. L’automatisation du calage est alors bien souvent préférée, d’autant plus avec l’essor des fonctions d’optimisation et de l’apprentissage automatique (machine learning) permettant d’obtenir des modèles plus performants et réalistes.
Une fois calibré, le modèle hydrologique est évalué dans des conditions différentes de celles où il a été calibré, sur une période appelée validation (voir la FAQ ci-dessous).
Définition
Après la calibration, un modèle hydrologique est soumis à une dernière étape : la validation. Il s’agit d’une phase d’évaluation de sa performance, c’est-à-dire, sa capacité à reproduire des simulations « suffisamment précises » dans des conditions différentes de celles de sa construction bien que le terme « suffisamment précis » puisse varier selon les objectifs de modélisation.
En général, la performance est évaluée en comparant les valeurs de débit simulées aux données de référence mesurées. Cette comparaison peut être effectuée qualitativement en confrontant les représentations graphiques des séries temporelles (e.g., les hydrogrammes) ou quantitativement à l’aide de critères statistiques. Ces critères évaluent l’erreur de la simulation, c’est-à-dire, la différence entre les valeurs de débit simulées et les valeurs observées.
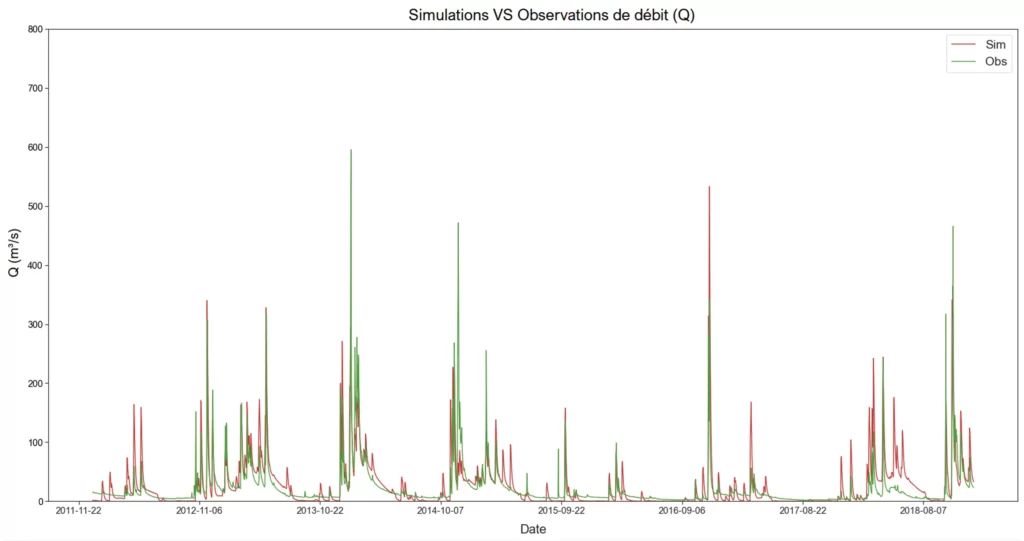
La performance peut être évaluée sur une période complète d’observations (e.g., quelques années de débits) ou sur des périodes spécifiques (e.g., période de crue, période de sècheresse) selon l’objectif de la modélisation (restitution de séries chronologiques, simulation d’évènements extrêmes hydrologiques, etc.).
Critères d’évaluation
Il existe de nombreux critères d’évaluation de la performance des modèles hydrologiques ; les plus couramment employés sont les suivants :
- NSE : Le coefficient d’efficacité du modèle de Nash – Sutcliffe [1]
Basé sur l’erreur quadratique moyenne, le NSE est l’indicateur le plus couramment utilisé. Les valeurs de NSE sont comprises dans l’intervalle ]-∞;1]. Plus la valeur du NSE est proche de 1, meilleure est l’adéquation du modèle aux observations.
- KGE : Le coefficient d’efficacité de Kling-Gupta [2]
Variante du NSE basé sur la décomposition en trois composantes (le biais, la variance et le coefficient de corrélation), qui permet d’estimer la variabilité et de moins sous-estimer les forts débits [3]. Ici aussi, une valeur du KGE proche de 1 indique une meilleure adéquation entre le modèle et les observations.
- pBIAS : Percent bias
Basé sur le biais (i.e., l’erreur moyenne), pBIAS mesure la fidélité du modèle à sous-estimer ou surestimer systématiquement les valeurs observées. Une valeur de pBIAS proche de 0 indique un modèle sans biais par rapport aux observations.
- RMSE : Racine de l’erreur quadratique moyenne
Basé sur la caractérisation de l’amplitude des écarts entre les observations et les simulations, le RMSE est un critère d’exactitude. Les valeurs du RMSE sont comprises dans l’intervalle [0;+∞[. Plus la valeur du RMSE est proche de zéro, meilleur est le modèle évalué en termes d’exactitude.
Chez Hydroclimat, pour évaluer la performance de nos modèles hydrologiques, nous utilisons une méthode multicritère qui combine l’ensemble de ces indicateurs afin de contrebalancer les limitations de chacun d’entre eux et d’obtenir une évaluation robuste et fiable de leur performance.
Références
[1] J. E. Nash et J. V. Sutcliffe, « River flow forecasting through conceptual models part I — A discussion of principles », Journal of Hydrology, vol. 10, no 3, p. 282‑290, avr. 1970, doi: 10.1016/0022-1694(70)90255-6.
[2] H. V. Gupta, H. Kling, K. K. Yilmaz, et G. F. Martinez, « Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling », Journal of Hydrology, vol. 377, no 1, p. 80‑91, oct. 2009, doi: 10.1016/j.jhydrol.2009.08.003.