Definition
A hydrological modelling is a simplified numerical representation of all or part of the processes of the water cycle (or hydrological cycle; Figure 1).

This cycle is based on the water balance, i.e., the balance between water inflows and outflows at the watershed scale (considered as a closed system). Overall, the inputs in a given time period are precipitation, which can then:
- Run off to rivers, lakes, and oceans,
- Return to the atmosphere via evapotranspiration,
- Recharge water reserves in soil, subsoil, and aquifers through infiltration.
The general water balance equation is as follows:
P = Q + E + D R
with P the amount of total precipitation (liquid and solid) on the catchment area; Q the proportion of water flowing through the hydrographic network; E the amount of water returned to the atmosphere by evapotranspiration, and R the change in water stockage in soil and subsoil layers.
A hydrological modelling quantifies the rainfall-runoff relationship at the watershed scale. It transforms climate time series (e.g., precipitation, temperature) into discharge time series; some models provide information on other hydrological processes (e.g., groundwater-river exchanges, groundwater flow, or snow cover) or complementary processes (e.g., water quality).
Applications
Hydrological modelling has many operational applications linked to the understanding, management, and planning of water resources. In particular, it can be used to:
- Reconstruct historical flow series,
- Model ungauged watersheds,
- Analyse the hydrological response of a watershed, i.e., how the watershed will react when it is subjected to precipitation,
- Provide streamflow, high and low flow forecasts,
- Assess the impact of climate and environmental changes on water resources,
- Monitor river water quality,
- Design and manage infrastructures and facilities, and
- Analyse the influence of human initiatives (e.g., dam construction, land artificialisation) on water resources and hydrological ecosystems.
At Hydroclimat, we use hydrological modelling to provide water data at high spatial resolution. This high value water data is suitable to forecast and predict long-term evolution of water resources and extremes (high and low flow) for water management and planning purposes.
A watershed is a complex hydrological system in which precipitation is transformed into flow through a series of interacting processes. Numerous hydrological models have been developed to represent the functioning of a watershed, each providing a simplified representation of the system, with its own advantages and limitations.
The hydrological models can be classified according to many criteria, but two of them are particularly used:
- The spatial discretization of the watershed, i.e., the way in which the watershed is represented as a single homogeneous entity (global model) or in hydrological sub-units (semi-distributed and distributed model), and
- The description of hydrological processes, either by empirical or physical equations, or by somewhat advanced simplification of the physical equations (conceptual approach).
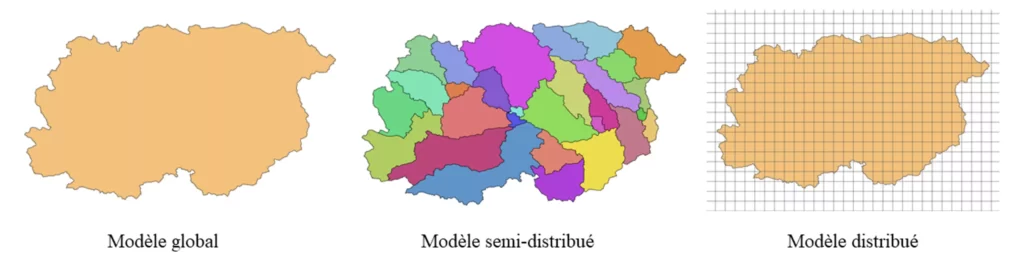
Three types of hydrological models can be differentiated according to the spatial discretization of the watershed:
- Global models (or lumped models): the watershed is described as a single homogeneous spatial entity, where the water balance is averaged over the entire basin, without taking into account the spatial variability of hydrological processes and input data.
- Semi-distributed models: the watershed is divided into several sub-basins. Each sub-basin is treated as a spatially homogeneous hydrological unit for which hydrological processes are calculated.
- Distributed models: the watershed is discretized into a regular or irregular grid. Hydrological processes are calculated for each grid cell. Distributed models are therefore more complex and more demanding in terms of input data and computation time.
The second classification criterion is linked to how the model represents hydrological processes; three types of hydrological models stand out:
Statistical or “data-driven” models: establish a mathematical relation between the input and output variables without considering physical characteristics of the watershed. These so-called “black-box” models are characterized by statistical parameters and relationships with no physical meaning. This is the main limitation of these models, which are inadequate to study watershed functioning or to explore climate change impacts on the watershed hydrology. They are, however, useful for real-time simulations, due to their rapid execution time, or for global analysis of the behaviour of a hydrosystem. Examples include stochastic models (e.g., auto-regression, linear regression, multiple regression), artificial neural networks (e.g., LSTM and GRU), Machine Learning and other techniques (wavelets, chaos theory, etc.).
Conceptual models: consider the watershed as several interlinked conceptual elements, basically a production store and a routing store. However, this type of model assumes empirical relationships between among different hydrological variables, which are often uncorrelated with the watershed characteristics. Parameter values are obtained by adjusting simulated flows to measured flows. As a result, conceptual models provide overall satisfactory flow simulations, but are unable to provide reliable simulations of other hydrological variables (i.e., evapotranspiration, infiltration, groundwater flow, etc.) that remain important in many applications. In addition, the analyse of human influence on hydrosystems and simulating the hydrological response in ungauged basins cannot be done with this model. Despite that, they are effective tools for specific applications such as regional water resource studies, streamflow forecasting as they require few input data.
Physically based models bridge the gap between statistical models, which are “too descriptive”, and conceptual models, which are “too simplistic” in terms of representation hydrological processes.. These models use physical equations to depict hydrological processes. The main advantage of the physically based models is that they use parameters with a physical meaning and can therefore provide valuable information on the various terms of the water balance (evapotranspiration, infiltration, recharge, etc.) of the watershed. Because of their ability to associate parameters with the climate and physical characteristics of watersheds, physical models are particularly suitable for interpreting and predicting the impacts of climate change on watershed hydrology. The main limitations of their application rely on the extensive input data requirements to estimate model parameters.
Criterion | Model type | Examples |
|---|---|---|
Watershed representation (discretization) | Global | WaterGAP [1]
|
Semi-distributed | SWAT [2], VIC [3]
| |
Distributed | G2G [4], MIKE SHE [5]
| |
Representation of hydrological processes | ||
Statistical | GR4J [6], Deep Learning-based models
| |
Conceptual | HBV [7], TOPMODEL [8]
| |
Physically based | SWAT [2], HYPE [9]
|
Table 1 – Examples of hydrological models according to the two classification criteria
The selection of the hydrological modelling type depends on the study objective and the available input data. At Hydroclimat, we use the SWAT model (Soil and Water Assessment Tool, [2]), a physically-based semi-distributed model that simulates the hydrological response of catchments of up to several thousand km at the daily time step (https://swat.tamu.edu/). The SWAT model is a flexible and robust tool, world-wide used to assess, among others, the impact of climate and land use change on water resources.
[1] H. Müller Schmied et al., « The global water resources and use model WaterGAP v2.2d: model description and evaluation », Geosci. Model Dev., vol. 14, no 2, p. 1037‑1079, févr. 2021, doi: 10.5194/gmd-14-1037-2021.
[2] S. L. Neitsch, J. G. Arnold, J. R. Kiniry, et J. R. Williams, « Soil and Water Assessment Tool Theoretical Documentation Version 2009 », Texas Water Resources Institute, Technical Report, sept. 2011. Consulté le: 10 avril 2023. [En ligne]. Disponible sur: https://oaktrust.library.tamu.edu/handle/1969.1/128050
[3] H. Wang, Z. Wu, et C. Hu, « A Comprehensive Study of the Effect of Input Data on Hydrology and non-point Source Pollution Modeling », Water Resour. Manag., vol. 29, no 5, p. 1505‑1521, mars 2015, doi: 10.1007/s11269-014-0890-x.
[4] V. A. Bell, A. L. Kay, R. G. Jones, et R. J. Moore, « Development of a high resolution grid-based river flow model for use with regional climate model output », Hydrol. Earth Syst. Sci., vol. 11, no 1, p. 532‑549, janv. 2007, doi: 10.5194/hess-11-532-2007.
[5] M. B. Abbott, J. C. Bathurst, J. A. Cunge, P. E. O’Connell, et J. Rasmussen, « An introduction to the European Hydrological System — Systeme Hydrologique Europeen, “SHE”, 1: History and philosophy of a physically-based, distributed modelling system », J. Hydrol., vol. 87, no 1, p. 45‑59, oct. 1986, doi: 10.1016/0022-1694(86)90114-9.
[6] C. Perrin, C. Michel, et V. Andréassian, « Improvement of a parsimonious model for streamflow simulation », J. Hydrol., vol. 279, no 1, p. 275‑289, août 2003, doi: 10.1016/S0022-1694(03)00225-7.
[7] S. BERGSTROM, « The HBV Model -its structure and applications », HBV Model -Its Struct. Appl., no 4, 1992.
[8] K. J. BEVEN et M. J. KIRKBY, « A physically based, variable contributing area model of basin hydrology / Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant », Hydrol. Sci. Bull., vol. 24, no 1, p. 43‑69, mars 1979, doi: 10.1080/02626667909491834.
[9] G. Lindström, C. Pers, J. Rosberg, J. Strömqvist, et B. Arheimer, « Development and testing of the HYPE (Hydrological Predictions for the Environment) water quality model for different spatial scales », Hydrol. Res., vol. 41, no 3‑4, p. 295‑319, avr. 2010, doi: 10.2166/nh.2010.007.
Hydrological models use physical laws for hydrological process representation at the watershed level. The processes are represented either by empirical equations or by differential equations based on hydrological principles, or an advanced simplification of physical equations. These equations involve parameters that need to be adjusted to provide an accurate and reliable simulation of streamflow. Calibration is the process by which the model parameters are adjusted so that the model simulations match the observations. The calibration step is carried out over a historical period for which observational data (e.g., streamflow) are available. A calibration period of several years is necessary to calibrate parameters over different seasons and for very different flow events.
There are two types of calibration:
- Manual calibration, which consists in manually modifying the model parameters individually and observing the effect on the flow simulation. The hydrologist uses its expertise to analyse the obtained hydrographs and adjust the model parameters to achieve an acceptable reproduction of the intensity and occurrence of peak flows, flood volumes, and base flows.
- Automatic calibration, which involves using an optimization algorithm to minimize the difference between simulated and observed flow values. The optimizers are based on iterative and intelligent methods that gradually modify model parameters and automatically determine the optimal values.
Manual calibration requires a good understanding of hydrological processes and their interactions. It is, however, subjective, tedious, and time-consuming, particularly when the model includes numerous parameters. Automatic calibration is therefore a better choice, especially with the rise of optimization functions and machine learning, which enable to obtain more performing and realistic models.
Once calibrated, the hydrological model is run on an independent period to assess the model’s actual performance under unknown conditions, called validation (see FAQ below).
Definition
After the calibration step, a hydrological modelling is subjected to a final stage: the validation This phase evaluates the performance of the calibrated model at reproducing the observations under different conditions from the calibration.
In general, model performance is assessed by comparing simulated flow values with measured flow data. This comparison can be made either qualitatively, by comparing graphical representations of time series (e.g., hydrographs), or quantitatively, using statistical criteria of model performance. The performance criteria evaluate the simulation errors, i.e., the differences between the simulated and observed flow values.
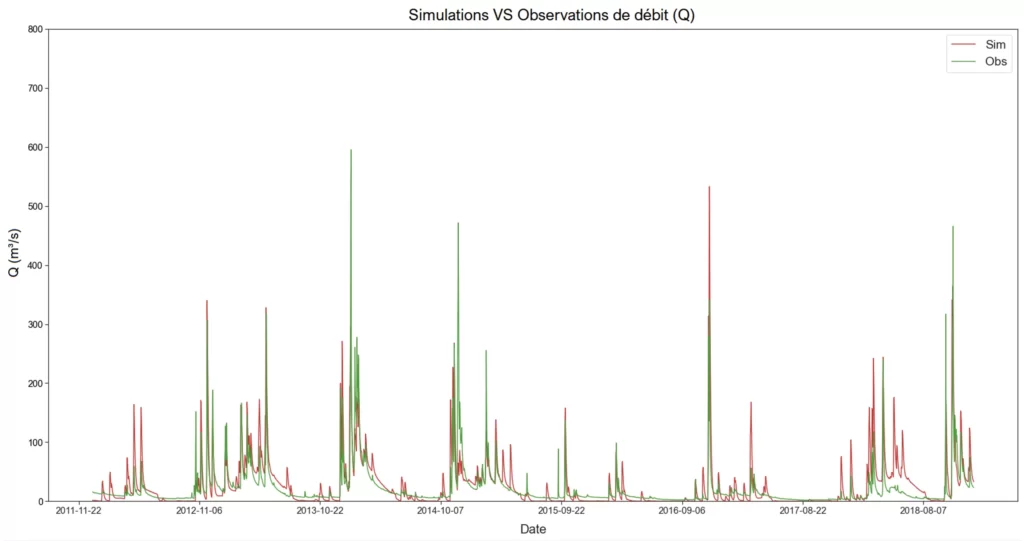
Model performance can be assessed over a complete period (e.g., a few years of flows) or over specific hydrological periods (e.g., flood and drought periods), depending on the modelling objective (i.e., restitution of time series, simulation of extreme hydrological events, etc.).
Evaluation criteria
There are many criteria for assessing the performance of hydrological models; the most commonly used criteria are:
- NSE : Nash–Sutcliffe model efficiency coefficient [1]
Based on the root mean square error, NSE is the most commonly used indicator. NSE values ranges from ]-∞;1]. NSE values nearer to 1 indicate a model with more predictive skill.
- KGE : King-Gupta efficiency coefficient [2]
Based on a three component of NSE of model errors (bias, variance, and correlation coefficient), KGE is extensively used for model performance as it allows variability to be estimated and high flows to be underestimated to a lesser extent [3]. KGE values close to 1 indicate a better fit between model simulations and observations.
- pBIAS: Percent bias
Based on bias (i.e., mean error), pBIAS measures the average tendency of the simulated values to be larger or smaller than the observed values. A pBIAS value close to 0 indicates an unbiased model with respect to observations.
- RMSE : Root Mean Square Error
Based on the quadratic mean of the differences between the simulated and observed values, RMSE is a criterion of model accuracy. RMSE values range from [0;+∞[, and a value close to 0 indicates a perfect fit of the model.
At Hydroclimat, we use a multi-criteria method to evaluate the performance of the hydrological models. The multi-criteria method combines the four above criteria to counterbalance each of their limitations to obtain a complete rational performance criterion for hydrological modelling.
References
[1] J. E. Nash et J. V. Sutcliffe, « River flow forecasting through conceptual models part I — A discussion of principles », Journal of Hydrology, vol. 10, no 3, p. 282‑290, avr. 1970, doi: 10.1016/0022-1694(70)90255-6.
[2] H. V. Gupta, H. Kling, K. K. Yilmaz, et G. F. Martinez, « Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling », Journal of Hydrology, vol. 377, no 1, p. 80‑91, oct. 2009, doi: 10.1016/j.jhydrol.2009.08.003.